这篇文章内容主要是来源于[1]这篇文章，这篇文章主要是一篇对衡量轨迹之间相似度的综述论文，在此我总结一下提一提干货。

概念

轨迹采样点：轨迹采样点包括经纬度和时间戳，按照一定规则从实际目标中采样而来，类似于((116.364629,39.940511), 3/1/2012 12:00:31 AM)，具体格式不重要，信息量一样。

轨迹距离：轨迹距离是衡量轨迹相似度的评价指标，轨迹距离越大，说明两个轨迹差距越大，反之则越相似。

轨迹距离可度量性：如果一种轨迹距离定义能够符合以下几点，即为具有可度量性：

  1. 非负性：$d(T_1,T_2) \geq 0$
  2. 同一性：$d(T_1,T_2)=0 \Leftrightarrow T_1=T_2$
  3. 对称性：$d(T_1,T_2)= d(T_2,T_1)$
  4. 三角不等性：$d(T_1,T_3) \leq d(T_1,T_2) + d(T_2,T_3)$

轨迹距离算法分类

  1. 针对离散轨迹or针对连续轨迹
  2. 部分采样点匹配or全部采样点匹配
  3. 是否具有可度量性
  4. 考虑时间信息or仅考虑位置信息
  5. 是否需要手动设置参数

后面各个算法我也按照这几点总结。

论文中的分类原图：

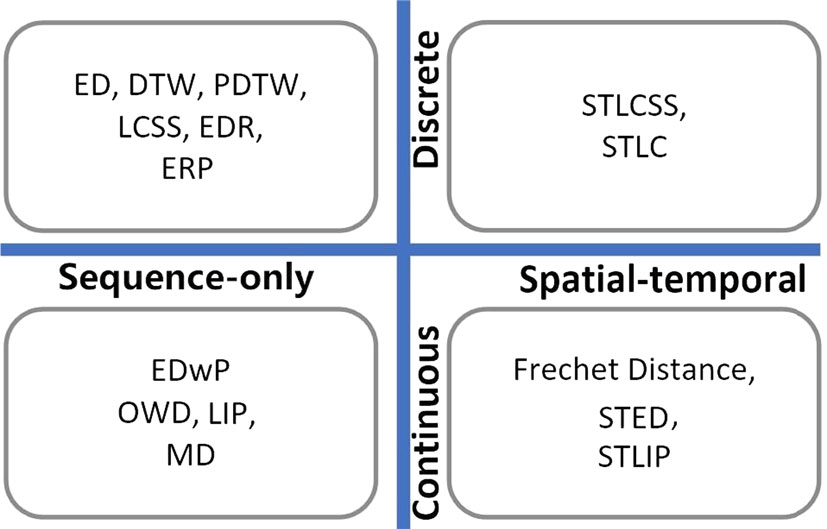
1618503148845

欧几里得距离(Euclidean distance)

非常经典的距离算法，是我们日常生活中最常用的距离算法了，原版为$d_{Euclidean}(T_1,T_2)=\frac {\Sigma_{i=1}^{n}d(p_{1,i},p_{2,i})} {n}$，不过这里需要两个轨迹的长度完全一致，不一致时匹配方法可以用$d_{Euclidean}(T_1,T_2)=\min \limits_{j=1}^{m-n+1} \frac {\Sigma_{i=1}^{n}d(p_{1,i},p_{2,j+i})} {n}$

  • 针对离散型轨迹
  • 全部采样点匹配
  • 具有可度量性
  • 仅考虑位置信息
  • 不需要手动设定参数
  • 相同长度的版本时间复杂度为$O(n)$，不同长度版本的时间复杂度为$O(mn)$
  • 对于误差有一定容忍性

DTW距离（Dynamic time warping）

DTW距离是非常经典的序列相似度匹配的算法，之前我在老博客命令词识别里详细讲过该算法，并且将该算法用于语音中的命令词识别，有兴趣的可以去看一看。

这里直接列公式 $$ d_{DTW}(T_1,T_2)= \begin{align*} 0 & & if \ n = 0 \ and\ m=0 \\
& \infty & & if \ n = 0 \ or\ m=0 \\
& d(Head(T_1),Head(T_2)+min \{ d_{DTW}(T1,Rest(T_2)),d_{DTW}(Rest(T_1),T_2),d_{DTW}(Rest(T_1),Rest(T_2))\}) & & otherwise\\
\end{align*} $$

  • 针对离散型轨迹
  • 全部采样点匹配
  • 不具有可度量性
  • 仅考虑位置信息
  • 不需要手动设定参数
  • 原版DTW的时间复杂度为$O(mn)$，改进速度版本PDTW时间复杂度为$O(\frac {MN} {c^2})$，$c$为抽样间隔
  • 对于误差有一定容忍性

最长公共子序列距离（LCSS distance）

LCSS算法是字符串的经典算法，算法导论里也有讲解，在这里的关键在于两个点位之间的匹配。字符串里的字符a仅会和a匹配，而轨迹中的匹配必定是模糊匹配，这就要求设计者要设置点位误差范围，当两个点的距离小于这个误差范围的时候，就当做两个点相同，然后就是LCSS算法的常规操作。 $$ s_{LCSS}(T_1,T_2)= \begin{align*} \Phi & & if \ i = 0 \ or\ j=0 \\
& s_{LCSS}(Rest(T_1),Rest(T_2))+1 & & if \ d(Head(T_1),Head(T_2)) \leq \epsilon \\
& max\{s_{LCSS}(T_1,Rest(T_2)),s_{LCSS}(Rest(T_1),T_2)\} & & otherwise\\
\end{align*} $$

LCSS距离$d_{LCSS}(T_1,T_2) = size(T_1)+size(T_2)-2*s_{LCSS}(T_1,T_2)$

正则化的LCSS距离$d_{LCSS}(T_1,T_2) = 1- \frac {s_{LCSS}(T_1,T_2)} {size(T_1)+size(T_2)-2*s_{LCSS}(T_1,T_2)}$

  • 针对离散型轨迹
  • 部分采样点匹配
  • 不具有可度量性
  • 仅考虑位置信息
  • 需要手动设定参数（点位允许误差）
  • 时间复杂度为$O(mn)$
  • 对于误差敏感

实序列编辑距离EDR distance（Edit distance on real sequence）

EDR算法是基于编辑距离的一种轨迹相似度度量算法，编辑距离算法和前面最长公共子序列一样，原本都是用于字符串相似度匹配的，用于轨迹匹配时，就要进行点位模糊匹配，需要设计者给定一个容许误差范围，在此误差范围内即认为两个点相同。匹配时就按照经典的编辑距离进行度量，其他不变。

$$ subcost(p_1,p_2) = \begin{align*} 0, & & d(p_1,p_2) \leq \epsilon \\
1, & & otherwise \\
\end{align*} $$

$$ d_{EDR}(T_1,T_2) = \begin{align*} n, & & if \ m = 0 \\
m, & & if \ n =0 \\
min \ \{ d_{EDR}(Rest(T_1),Rest(T_2))+subcost(Head(T_1),Head(T_2)), d_{EDR}(Rest(T_1),T_2)+1,d_{EDR}(T_1,Rest(T_2))+1 \} & & otherwise \end{align*} $$

  • 针对离散型轨迹
  • 部分采样点匹配
  • 不具有可度量性
  • 仅考虑位置信息
  • 需要手动设定参数（点位允许误差）
  • 时间复杂度为$O(mn)$
  • 对于误差不敏感

带惩罚的编辑距离（Edit distance with real penalty）

ERP算法也是基于编辑距离的一种算法，它的特点是将编辑距离匹配中的插入、删除操作中缺少值的一方，看作一个gap算子。具体来说，$T_1$和$T_2$匹配，其中如果要对$T_1$插入一个来自于$T_2$的$p_j$使其更接近$T_2$，那么在匹配时$p_j$这个点对应的就是$T_1$的一个gap算子，表示没有对应的值匹配。相反地，如果要对$T_1$删除一个$p_i$来使$T_1$更接近$T_2$，那么匹配时$p_i$这个点对应的就是$T_2$的一个gap算子。在匹配时，这个gap算子的距离需要设计者自己设置。

编辑距离具体匹配时按照以下规则：

$$ dist_{ERP}(p_1,p_2) = \begin{align*} |p_1 - p_2|, & & if \ p_1,p_2 \ not \ gaps \\
|p_1 - g|, & & if \ p_2 \ is \ a \ gap \\
|p_2 - g|, & & if \ p_1 \ is \ a \ gap \end{align*} $$

ERP算法的距离表示为

$$ d_{ERP}(p_1,p_2) = \begin{align*} \Sigma_{1}^{n}dist_{ERP}(p_{1,i},g), & & if \ m = 0 \\
\Sigma_{1}^{m}dist_{ERP}(p_{2,i},g), & & if \ n = 0 \\
min\{d_{ERP}(Rest(T_1),Rest(T_2))+dist_{ERP}(Head(T_1),Head(T_2)), \\
d_{ERP}(Rest(T_1),T_2)+dist_{ERP}(Head(T_1),g),\\
d_ERP(T_1,Rest(T_2))+dist_{ERP}(Head(T_2),g)\}, & & otherwise \end{align*} $$

  • 针对离散型轨迹
  • 部分采样点匹配
  • 具有可度量性
  • 仅考虑位置信息
  • 需要手动设定参数(gap值)
  • 时间复杂度为$O(mn)$
  • 对误差不敏感

投影编辑距离（Edit distance with projections）

这个我个人感觉糟的一塌糊涂，实无应用之可能，有兴趣自己查吧

单向距离（One-way distance）

这算法的核心宗旨是计算在$T_1$上的每个点到$T_2$的最短距离，然后求平均值（自己愿意也可以加权）。点到轨迹的最短距离就取轨迹上与这个点最近的一个点，然后计算这两个点的距离当做点到轨迹的距离。很明显，这样一来$T_1$到$T_2$的距离可未必等于$T_2$到$T_1$的距离。公式表示如下：

$点到轨迹距离d_{point}(p,T) = \min\limits_{p’ \in T}d(p,p’)$

$单向距离d_{owd}(T_1 \rightarrow T) = \frac {1} {Size(T_1)} *\mathop\Sigma\limits_{p \in T_1} d_{point}(p,T_2)$

$双向距离d_{OWD}(T_1,T_2) = 0.5 * (d_{owd}(T_1 \rightarrow T_2) + d_{owd}(T_2 \rightarrow T_1)$

  • 离散连续均可
  • 所有采样点匹配
  • 不具有可度量性
  • 仅考虑位置信息
  • 不需要手动设定参数
  • 时间复杂度为$O(mn)$
  • 对误差不敏感

多边形面积距离（Locality in-between polylines distance）

这个算法跳出了前面将轨迹计算化为点的计算的模式，改为计算两个轨迹之间围成的多边形的面积。

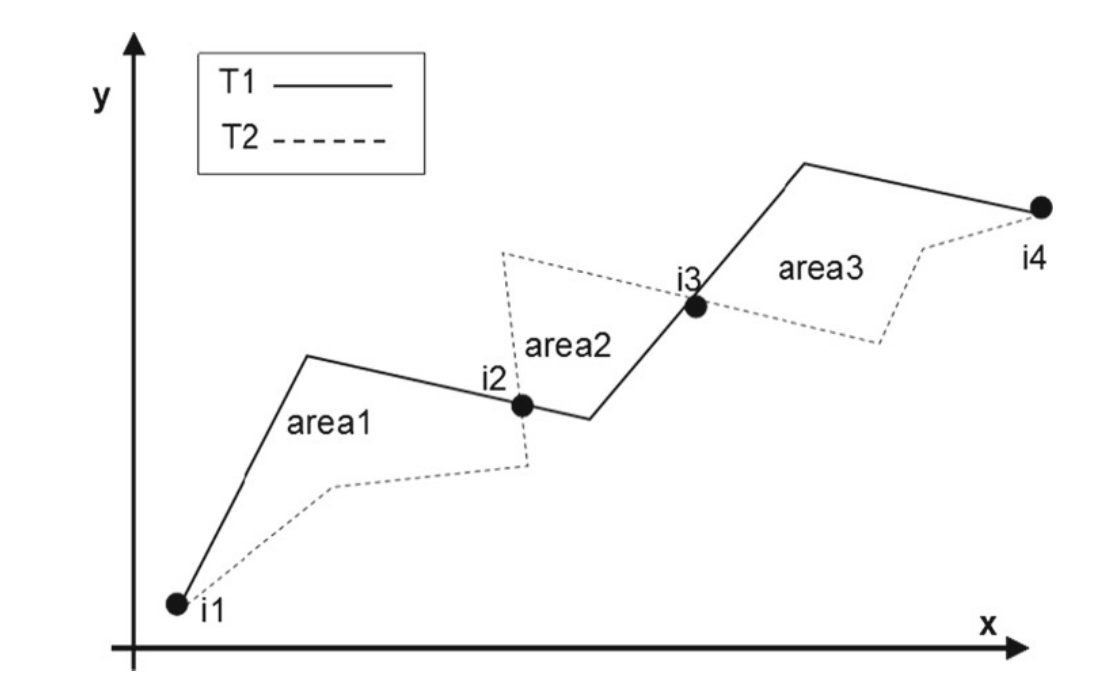
1618817319610

$d_{LIP}(T_1,T_2) = \mathop\Sigma\limits_{\forall polygon_i}Area_i * w_i$

$w_k = \frac {Length_{T_1}(i_k,i_{k+1}) + Length_{T_2}(i_k,i_{k+1})} {Length(T_1) + Length(T_2)}$

这个算法就相当于计算差异面积的加权和。不过对于下面这两种情况没办法正确计算：

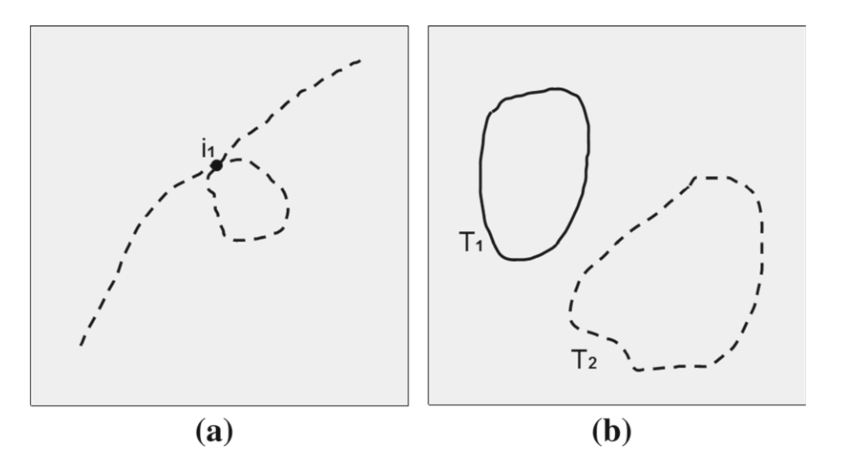
1618817859722

  • 离散连续均可
  • 所有采样点匹配
  • 不具有可度量性
  • 仅考虑位置信息
  • 不需要手动设定参数
  • 时间复杂度为$O((m+n) * log(m+n))$
  • 对误差敏感度较高

距离归并算法（Merge distance）

这个算法的核心是把两个轨迹合并成一个中间轨迹，然后计算这个中间轨迹和两条原轨迹的差异作为两条轨迹的距离。

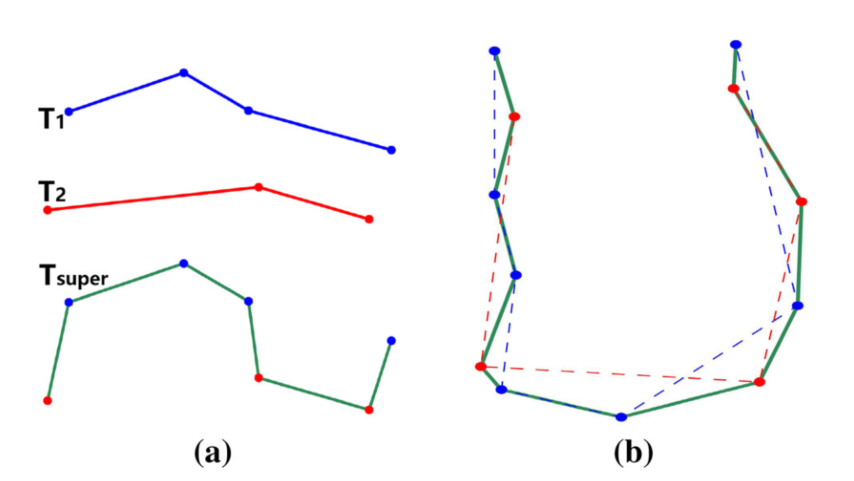
1618818812289

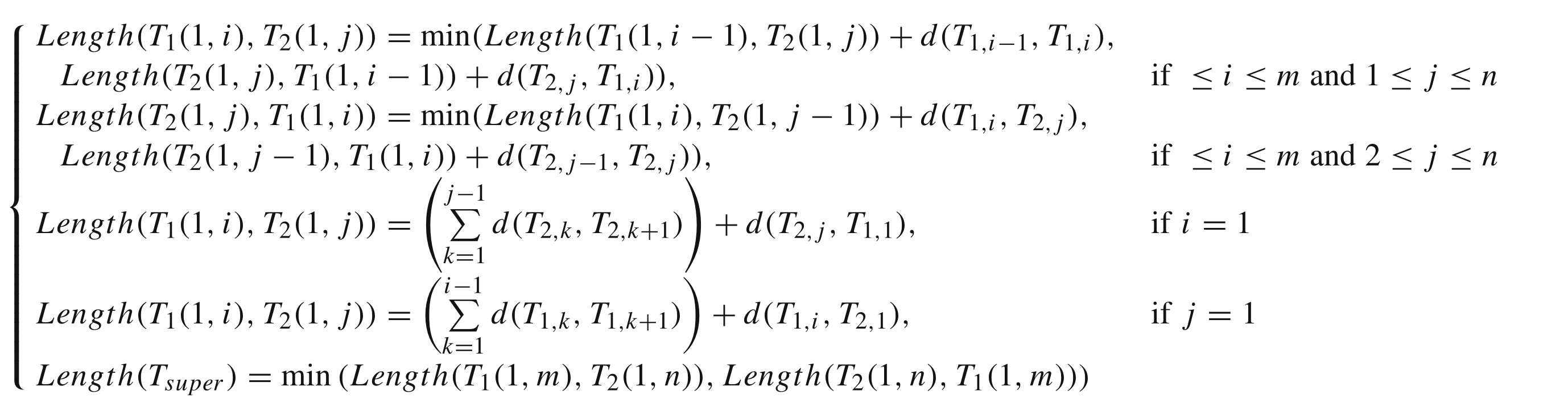
1618818856530

$d_{MD}(T_1,T_2) = \frac {Length(T_{super})} {Length(T_1) + Length(T_2)} - 1$

  • 离散连续均可
  • 所有采样点匹配
  • 不具有可度量性
  • 仅考虑位置信息
  • 不需要手动设定参数
  • 时间复杂度为$O(mn)$
  • 对于误差有一定容忍性

时空最长公共子序列距离（Spatiotemporal LCSS）

和前面的最长公共子序列距离很类似，不过这回增加考虑了时间这个因素。原本是设定一个距离误差范围，小于这个误差范围的就算这两个点匹配上了。现在是再增加一个时间误差范围，在前面的要求上额外要求时间差必须在这个误差范围才算匹配得上。

设$\epsilon$为距离误差范围，$\delta$为时间误差范围，匹配方式如下图所示：

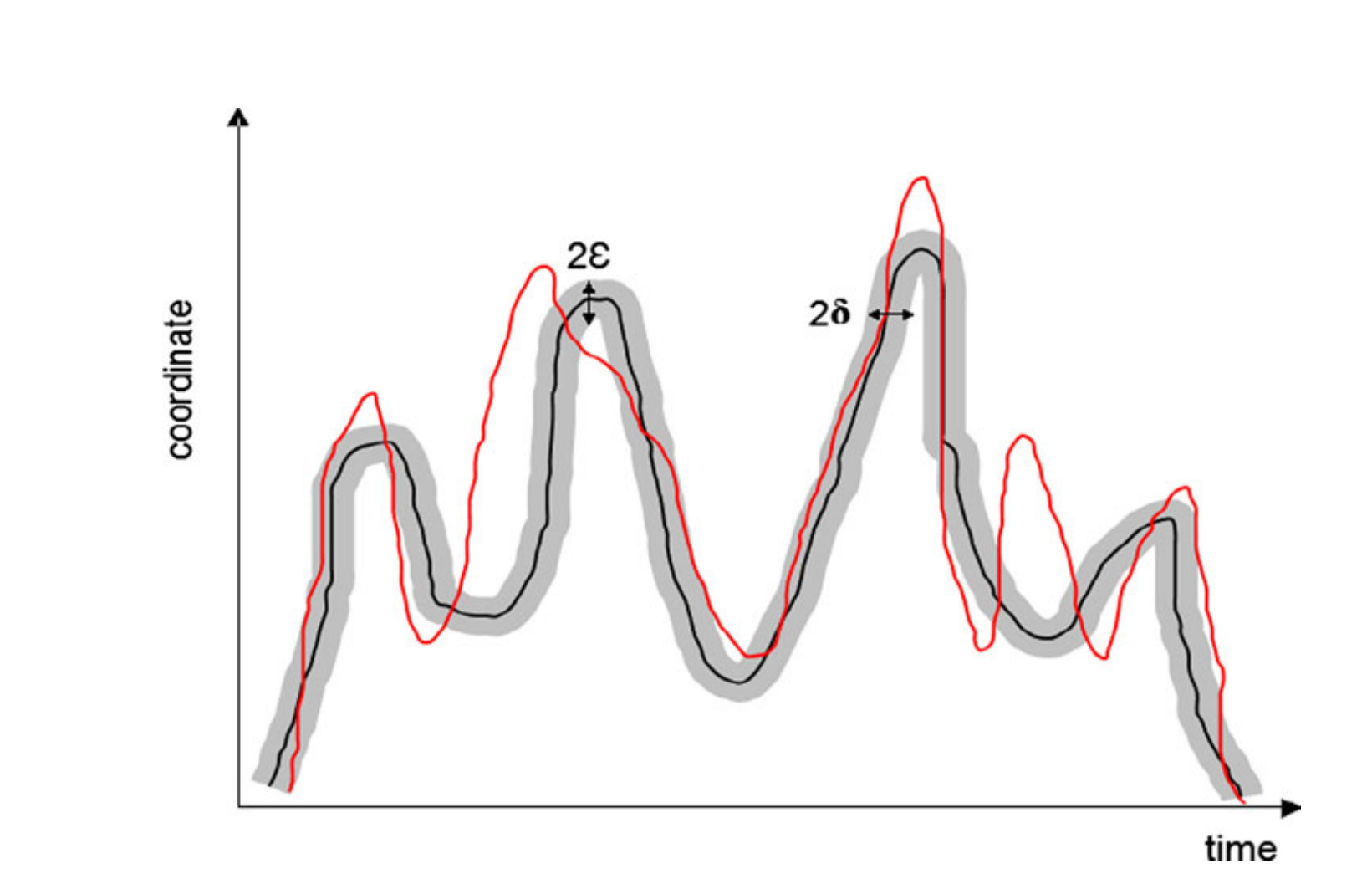
1618819637835

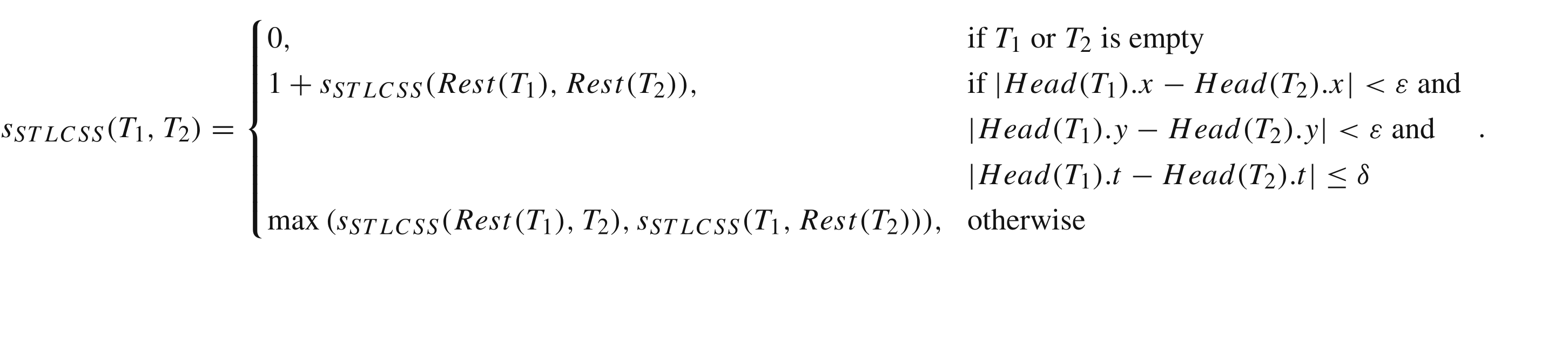
1618819746963

$d_{STLCSS}(T_1,T_2) = 1 - \frac {s_{STLCSS}(T_1,T_2)} {min(n,m)}$

  • 针对离散型轨迹
  • 部分采样点匹配
  • 不具有可度量性
  • 同时考虑时间和位置信息
  • 需要手动设定参数
  • 时间复杂度为$O(mn)$
  • 对于误差有一定容忍性

时空线性结合距离（Spatiotemporal linear combine distance）

这个算法的思路是将时间和时间匹配、位置和位置匹配，最后按照一定权值线性组合起时间距离和空间距离，作为总体的轨迹距离。

$d_{spa}(p,T) = \min\limits_{p’ \in T}{d(p,p’)}$

$d_{tem}(p,T) = \min\limits_{p’ \in T}{|p_{.t} - p’_{.t}|}$

$s_{spa}(T_1,T_2) = \frac {\Sigma_{p \in T_1}e^{-d_{spa}(p,T_2)}} {Size(T_1)} + \frac {\Sigma_{p \in T_2}e^{-d_{spa}(p,T_1)}} {Size(T_2)}$

$s_{tem}(T_1,T_2) = \frac {\Sigma_{p \in T_1}e^{-d_{tem}(p,T_2)}} {Size(T_1)} + \frac {\Sigma_{p \in T_2}e^{-d_{tem}(p,T_1)}} {Size(T_2)}$

$s_{spa}和s_{tem}的取值都在[0,2]区间$

$d_{STLC}(T_1,T_2) = \lambda*s_{spa}(T_1,T_2) + (1-\lambda)*s_{tem}(T_1,T_2)$

这里的$\lambda$是线性组合的加权值，$\lambda \in [0,1]$，表示空间距离和时间距离的权重设置。

  • 针对离散型轨迹
  • 全部采样点匹配
  • 不具有可度量性
  • 同时考虑时间和位置信息
  • 需要手动设定参数
  • 时间复杂度为$O(mn)$
  • 对于误差有一定容忍性

弗雷歇距离（Fréchet distance）

首先要说这个算法是针对连续的曲线进行匹配，其次是这个算法把匹配的距离和采样方式合并在一起考虑。

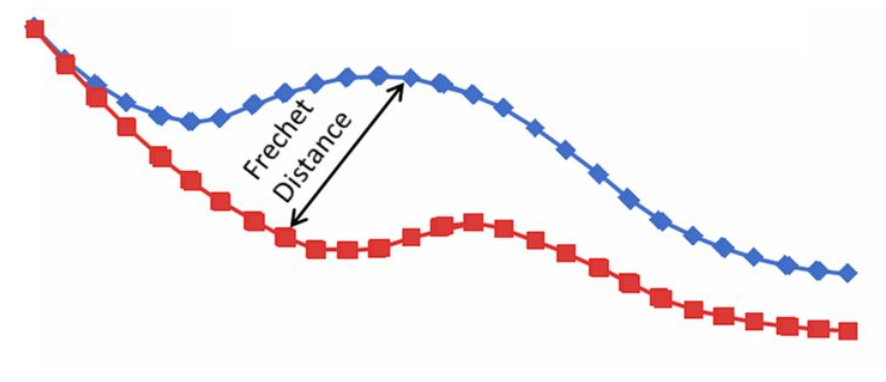
1618820691038

通俗地讲，要做匹配，咱先得想想如何采样？因为不采样就不能进行点位之间的计算。先这样想，我们任取一种采样方式，这个时候就和前面两个离散轨迹匹配问题是一样的了。然后计算同一时刻的两个轨迹上对应的采样点之间的距离，这时会有许多个点位对的距离值，取其中最大的一个作为这种采样方式下的两个轨迹的距离。那么回到采样方式上，我们就选取让轨迹距离最小化的时候的采样方式作为最后的采样方式。

看到网上还有种更简单的说法，这个算法的距离相当于遛狗的时候狗绳的长度，不管狗是近是远，最大距离就是狗绳的长度。

写成公式如下所示：

$d_{Fréchet}(T_1,T_2) = inf \max\limits_{t \in [t.start,t.end]}{d(f_1(t),f_2(t))}$

  • 针对连续型轨迹
  • 部分采样点匹配
  • 不具有可度量性
  • 同时考虑时间和位置信息
  • 不需要手动设定参数
  • 时间复杂度为$O(mn)$
  • 对于误差敏感

其他还有一些连续轨迹型的算法，在这就不写了。

哪种轨迹距离算法更好？

这篇文章这一节设计很有意思，因为上面这些算法从解决问题思路方式、匹配采样点模式、是否具有可度量性、是否考虑时间信息、是否需要额外设定参数等等差距极大，甚至连相似度的范围都有所不同，很难比较哪种算法更好。

于是文章作者想到了自己通过创造数据集来测试，数据集分为原始数据集和做过变换过的数据集，原始数据集为一些轨迹的集合，变换数据集为原始数据集中的轨迹进行变换操作后得到的略有差别的轨迹。变换操作主要有增加采样点、减少采样点、改变采样率、平移变换、增加噪声点这几种方式。如果一种轨迹距离算法可以把原始数据集和变换数据集中原本相同的轨迹匹配在一起，那就说明这种算法更理想。

一堆比较结果就不提了，按照这篇文章的说法，STLC算法在各个方面匹配度都高于其他算法，同时考虑到这些算法的时间复杂度大差不差一般都是$O(mn)$，所以一般情况下使用STLC算法可能是最合适的。

参考文献：

[1] :Su, H., Liu, S., Zheng, B. et al. A survey of trajectory distance measures and performance evaluation. The VLDB Journal 29, 3–32 (2020). https://doi.org/10.1007/s00778-019-00574-9