这个过滤器本身是一篇论文中提出的过滤器的简化版本,去掉了计数功能,我觉得简化版本应用的可能也很广,专门写一篇简化版本的RSQF。RSQF全称是rank-and-select based filter,一会我们会专门来讲这个rank-and-select是什么。
原论文可以到这里下载:http://www3.cs.stonybrook.edu/~ppandey/files/SIGMOD17_Talk_CQF_long.pdf
过滤器分下面几部分来讲
Hash函数
这部分不属于原论文,这部分假设有一个比较好的Hash函数,可以将原数据hash成n位数据,设n = q + r,这个r实际上控制着过滤器的假阳率和空间大小的平衡。假阳率是$2^{-r}$,当然如果r越大,空间消耗也越大
结构
结构部分如下图所示
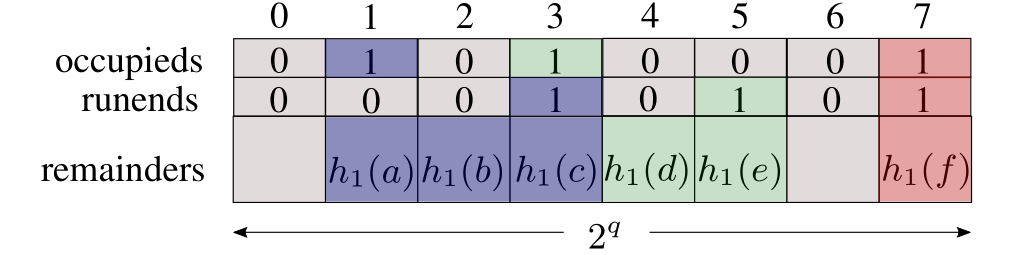
我们分别来介绍这个结构中的各部分,其中occupieds这一行是1bit数组,元素只能表示1或0;runends也是1bit数组;remainders内每个元素占用r个bit,就是前一部分说的r。这个块总共有$2^q$列,q也是前文说的q。
我们设某一列的下标为$i$,则当有元素hash后的前q位对应到这一列的时候,$occupieds[i] = 1$;我们把这个元素放到对应位置上,那么如果有多个元素对应这个位置,我们要求,把具有相同前q位的元素放到相邻位置。那么什么时候代表结束呢?就是这些前q位相同的元素的最后一个元素对应位置$runends[i] = 1$。在图中,相同颜色的元素其前q位是相同的,也就是说如果不考虑重复,他们都应该存在相同位置上的。
算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| def MAY_CONTAIN(Q,x)
"""
查找算法,Q代表存储结构,x代表要查找的元素
"""
b = h0(x) #计算hash值,取其前q位
if Q.occupieds[b] = 0:
return 0
t = RANK(Q.occupieds,b)
k = SELECT(Q.runends,t)
v = h(x) #计算hash值取其后r位
while k >= b and Q.runends[k] = 0:
if Q.remainders[k] = v:
return 1
k -= 1
return false
|
RANK(Q,i)是找到在位置i之前,数组Q中有多少个1出现过
SELECT(Q,i)是找到数组Q中第i次出现1的位置
先通过找到在某个位置之前在occupieds上有多少个1,就代表有多少组相同前q位hash值的元素组,然后通过runends的第i个1,找到目前这个位置对应的组,这样就可以精准定位。
1
2
3
4
5
6
7
8
9
10
11
| def find_first_unused_slot(Q,x):
"""
找到第一个空位置,以便于在插入元素时向后移动元素
"""
r = rank(Q.occupieds,x)
s = select(Q.runends)
while x < s:
x = s + 1
r = RANK(Q.occupieds,x)
s = SELECT(Q.runends,s)
return x
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| def insert(Q,x):
"""
插入一个元素
实质是先找到一个空位,然后把要插入位置之后的所有元素依次右移,直到把要插入位置空出来为止
"""
r = RANK(Q.occupieds,h0(x))
s = SELECT(Q.runends,r)
if h0(x) > s:
Q.remainders[h0(x)] = h1(x)
Q.runends[h0(x)] = 1
else:
s += 1
n = find_first_unused_slot(Q,s)
while n > s:
Q.remainders[n] = Q.remainers[n-1]
Q.runends[n] = Q.remainers[n-1]
n -= 1
Q.remainers[s] = h1(x)
if Q.occupieds[h0(x)] == 1:
Q.runends[s-1] = 0
Q.runends[s] = 1
Q.occupieds[h0(x)] = 1
return
|
原论文中其实还有一个在块内加速的一个索引方式,在这里没有讲到,想要详细了解的可以看原论文。如果想要看带计数功能版本的过滤器也请看原论文,github上也有公开代码。https://github.com/splatlab/cqf
