什么是KD树
要说KD树，我们得先说一下什么是KNN算法。
KNN是k-NearestNeighbor的简称，原理很简单：当你有一堆已经标注好的数据时，你知道哪些是正类，哪些是负类。当新拿到一个没有标注的数据时，你想知道它是哪一类的。只要找到它的邻居（离它距离短）的点是什么类别的，所谓近朱者赤近墨者黑，KNN就是采用了类似的方法。
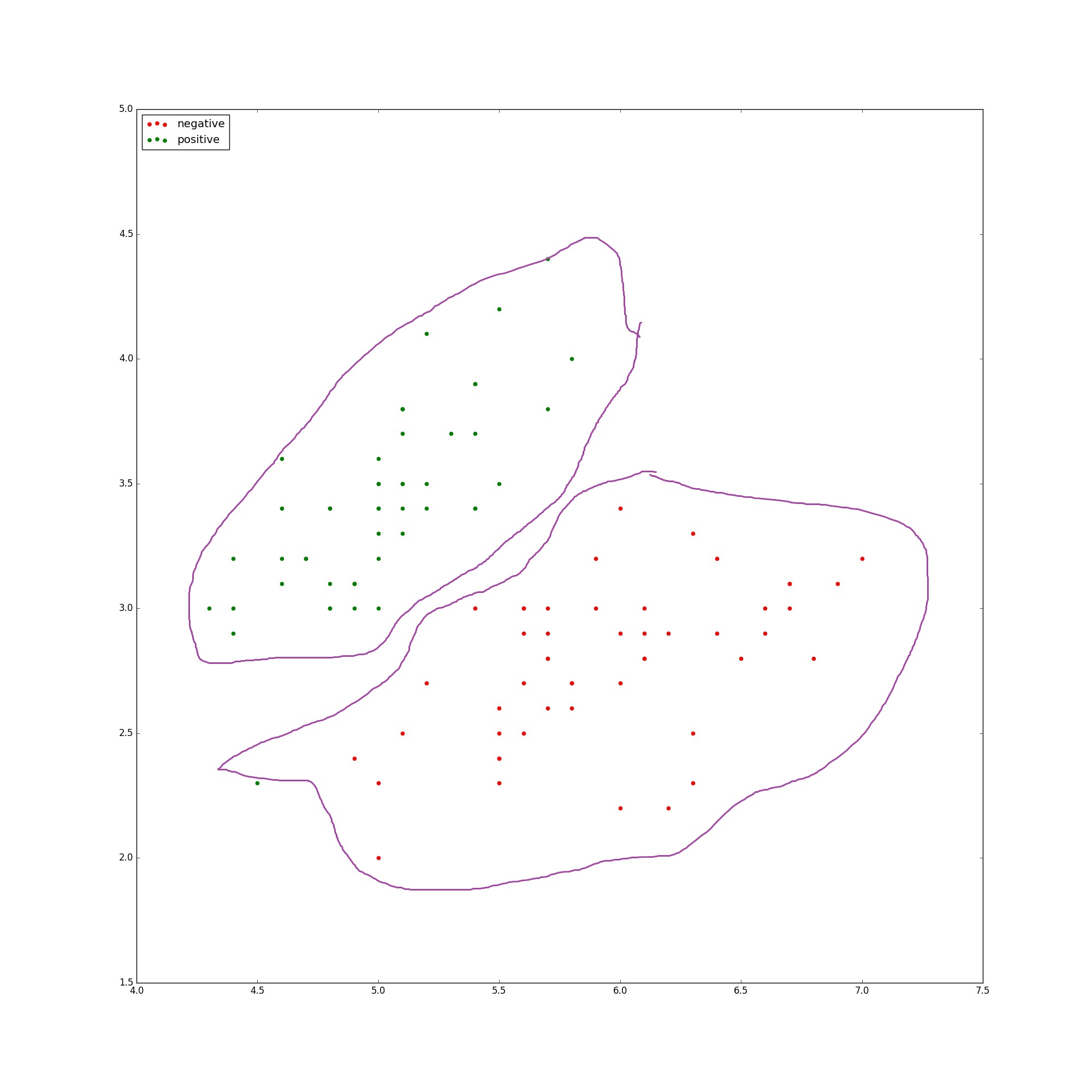
如上图，当有新的点不知道是哪一类时，只要看看离它最近的几个点是什么类别，我们就判断它是什么类别。
举个例子：我们将k取3（就是每次看看新来的数据点的三个住的最近的邻居），那么我们将所有数据点和新来的数据点计算一次距离，然后排序，取前三个数据点，让它们举手表决。两票及以上的类别我们就认为是新的数据点的类别。
很简单也很好的想法，但是，我们要注意到当测试集数据比较大时，由于每次未标注的数据点都要和全部的已标注的数据点进行一次距离计算，然后排序。可以说时间开销非常大。我们在此基础上，想到了一种存储点与点之间关系的算法来通过空间换时间。
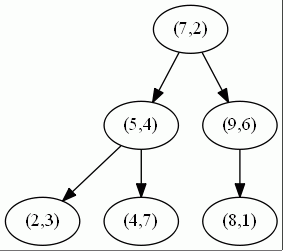
举个例子：有一个二维的数据集: T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}
通过你已经学习的KD树的算法，按照依次选择维度，取各维中位数，是否得出和下面一样的KD树？
异常检测
我们的数据来自于KDD Cup 1999 Data 点我下载数据
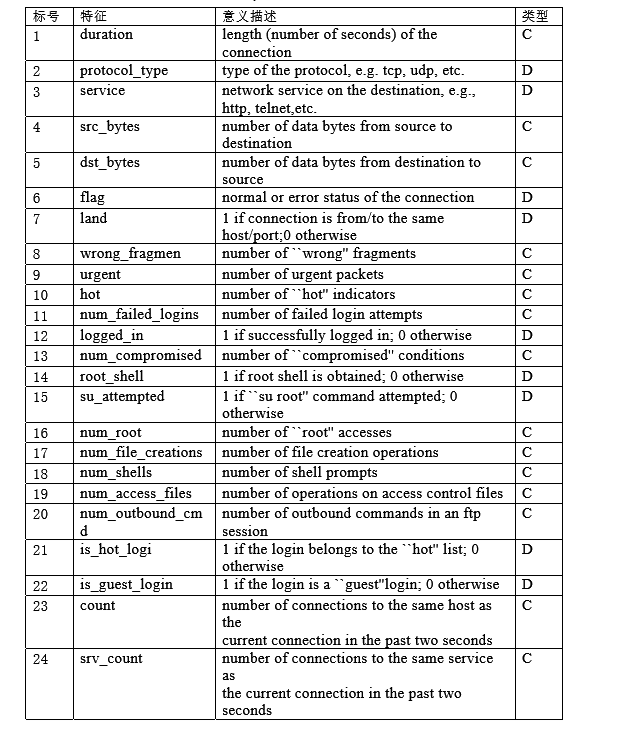
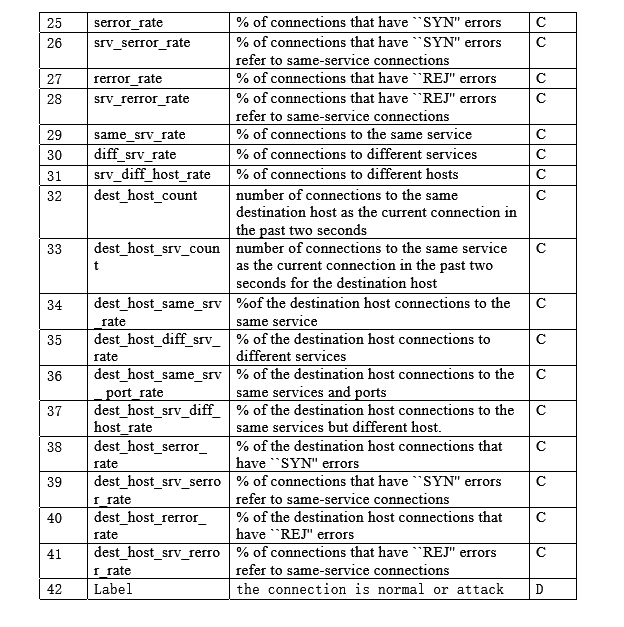
数据格式如下图
数据的含义如下：
我们这次实验针对正常和DDOS攻击两种情况进行检测。
取特征范围为(1,9)U(22,31)的特征中的数值型特征，最终得到16维的特征向量。将数据随机化处理后按照7:3的比例分成训练集和测试集。下面是我们组做好的训练集和测试集
点我下载
处理完的训练集和测试集如下图：
下面是具体实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| # coding=utf8
import math
import time
import matplotlib.pyplot as plt
import numpy as np
old_settings = np.seterr(all='ignore')
#定义节点类型
class KD_node:
def __init__(self, point=None, split=None, left=None, right=None):
'''
:param point: 数据点的特征向量
:param split: 切分的维度
:param left: 左儿子
:param right: 右儿子
'''
self.point = point
self.split = split
self.left = left
self.right = right
|
计算方差，以利用方差大小进行判断在哪一维进行切分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| def computeVariance(arrayList):
'''
:param arrayList: 所有数据某一维的向量
:return: 返回
'''
for ele in arrayList:
ele = float(ele)
LEN = float(len(arrayList))
array = np.array(arrayList)
sum1 = float(array.sum())
array2 = np.dot(array, array.T)
sum2 = float(array2.sum())
mean = sum1 / LEN
variance = sum2 / LEN - mean ** 2
return variance
|
建树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| def createKDTree(root, data_list):
'''
:param root: 输入一个根节点，以此建树
:param data_list: 数据列表
:return: 返回根节点
'''
LEN = len(data_list)
if LEN == 0:
return
# 数据点的维度
dimension = len(data_list[0]) - 1 #去掉了最后一维标签维
# 方差
max_var = 0
# 最后选择的划分域
split = 0
for i in range(dimension):
ll = []
for t in data_list:
ll.append(t[i])
var = computeVariance(ll) #计算出在这一维的方差大小
if var > max_var:
max_var = var
split = i
# 根据划分域的数据对数据点进行排序
data_list = list(data_list)
data_list.sort(key=lambda x: x[split]) #按照在切分维度上的大小进行排序
data_list = np.array(data_list)
# 选择下标为len / 2的点作为分割点
point = data_list[LEN / 2]
root = KD_node(point, split)
root.left = createKDTree(root.left, data_list[0:(LEN / 2)])#递归的对切分到左儿子和右儿子的数据再建树
root.right = createKDTree(root.right, data_list[(LEN / 2 + 1):LEN])
return root
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| def computeDist(pt1, pt2):
'''
:param pt1: 特征向量1
:param pt2: 特征向量2
:return: 两个向量的欧氏距离
'''
sum_dis = 0.0
for i in range(len(pt1)):
sum_dis += (pt1[i] - pt2[i]) ** 2
#实现的欧氏距离计算，效率很低的版本，可以改成numpy的向量运算
return math.sqrt(sum_dis)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| def findNN(root, query):
'''
:param root: 建立好的KD树的树根
:param query: 查询数据
:return: 与这个数据最近的前三个节点
'''
# 初始化为root的节点
NN = root.point
min_dist = computeDist(query, NN)
nodeList = []
temp_root = root
dist_list = [temp_root.point, None, None] #用来存储前三个节点
##二分查找建立路径
while temp_root:
nodeList.append(temp_root) #对向下走的路径进行压栈处理
dd = computeDist(query, temp_root.point) #计算当前最近节点和查询点的距离大小
if min_dist > dd:
NN = temp_root.point
min_dist = dd
# 当前节点的划分域
temp_split = temp_root.split
if query[temp_split] <= temp_root.point[temp_split]:
temp_root = temp_root.left
else:
temp_root = temp_root.right
##回溯查找
while nodeList:
back_point = nodeList.pop()
back_split = back_point.split
if dist_list[1] is None:
dist_list[2] = dist_list[1]
dist_list[1] = back_point.point
elif dist_list[2] is None:
dist_list[2] = back_point.point
if abs(query[back_split] - back_point.point[back_split]) < min_dist:
#当查询点和回溯点的距离小于当前最小距离时，另一个区域有希望存在更近的节点
#如果大于这个距离，可以理解为假设在二维空间上，直角三角形的直角边已经不满足要求了，那么斜边也一定不满足要求
if query[back_split] < back_point.point[back_split]:
temp_root = back_point.right
else:
temp_root = back_point.left
if temp_root:
nodeList.append(temp_root)
curDist = computeDist(query, temp_root.point)
if min_dist > curDist:
min_dist = curDist
dist_list[2] = dist_list[1]
dist_list[1] = dist_list[0]
dist_list[0] = temp_root.point
elif dist_list[1] is None or curDist < computeDist(dist_list[1], query):
dist_list[2] = dist_list[1]
dist_list[1] = temp_root.point
elif dist_list[2] is None or curDist < computeDist(dist_list[1], query):
dist_list[2] = temp_root.point
return dist_list
|
进行判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| def judge_if_normal(dist_list):
'''
:param dist_list: 利用findNN查找出的最近三个节点进行投票表决
:return:
'''
normal_times = 0
except_times = 0
for i in dist_list:
if abs(i[-1] - 0.0) < 1e-7: #浮点数的比较
normal_times += 1
else:
except_times += 1
if normal_times > except_times: #判断是normal
return True
else:
return False
|
数据预处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| def pre_data(path):
f = open(path)
lines = f.readlines()
f.close()
lstall = []
for line in lines:
lstn = []
lst = line.split(",")
u = 0
y = 0
for i in range(0, 9):
if lst[i].isdigit():
lstn.append(float(lst[i]))
u += 1
else:
pass
for j in range(21, 31):
try:
lstn.append(float(lst[j]))
y += 1
except:
pass
if lst[len(lst) - 1] == "smurf.\n" or lst[len(lst) - 1] == "teardrop.\n":
lstn.append(int("1"))
else:
lstn.append(int("0"))
lstall.append(lstn)
nplst = np.array(lstall, dtype=np.float16)
return nplst
|
下面就是个人的测试代码了，大概运行了40分钟才全跑完
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| def my_test(all_train_data, all_test_data, train_data_num):
train_data = all_train_data[:train_data_num]
train_time_start = time.time()
root = KD_node()
root = createKDTree(root, train_data)
train_time_end = time.time()
train_time = train_time_end - train_time_start
right = 0
error = 0
test_time_start = time.time()
for i in range(len(all_test_data)):
if judge_if_normal(findNN(root, all_test_data[i])) is True and abs(all_test_data[i][-1] - 0.0) < 1e-7:
right += 1
elif judge_if_normal(findNN(root, all_test_data[i])) is False and abs(all_test_data[i][-1] - 1.0) < 1e-7:
right += 1
else:
error += 1
test_time_end = time.time()
test_time = test_time_end - test_time_start
right_ratio = float(right) / (right + error)
return right_ratio, train_time, test_time
def draw(train_num_list=[10, 100, 1000, 10000], train_data=[], test_data=[]):
train_time_list = []
test_time_list = []
right_ratio_list = []
for i in train_num_list:
print 'start run ' + i.__str__()
temp = my_test(train_data, test_data, i)
right_ratio_list.append(temp[0])
train_time_list.append(temp[1])
test_time_list.append(temp[2])
plt.title('train data num from ' + train_num_list[0].__str__() + ' to ' + train_num_list[:-1].__str__())
plt.subplot(311)
plt.plot(train_num_list, right_ratio_list, c='b')
plt.xlabel('train data num')
plt.ylabel('right ratio')
plt.grid(True)
plt.subplot(312)
plt.plot(train_num_list, train_time_list, c='r')
plt.xlabel('train data num')
plt.ylabel('time of train data (s)')
plt.grid(True)
plt.subplot(313)
plt.plot(train_num_list, test_time_list, c='g')
plt.xlabel('train data num')
plt.ylabel('time of test data (s)')
plt.grid(True)
plt.show()
data = pre_data('KDD-test\ddos+normal_70.txt')
data2 = pre_data('KDD-test\ddos+normal_30.txt')
'''
建议开始将测试数据调小点，因为时间很长，下面这是全部训练集和全部测试集，共花费了40分钟才跑完。我是第六代i7 6700HQ+16G内存+1070+win10
'''
draw(train_num_list=[10, 100, 500, 1000, 2000, 3000, 5000, 10000, 15000, 20000, 50000, 100000, 265300],
train_data=data[:], test_data=data2[:])
|
跑完的效果如图所示：
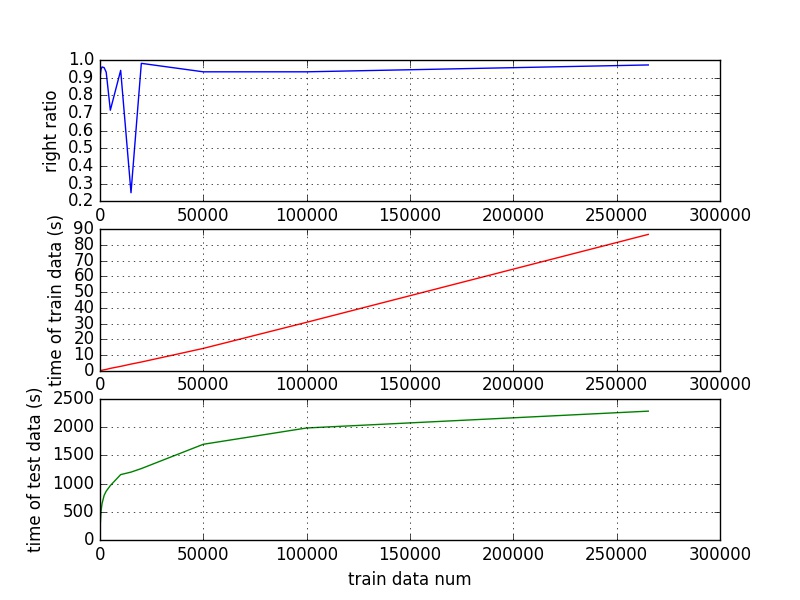正确率最终达到95%以上。开始出现的波动我们怀疑是数据在开始没有达到良好的随机效果。
训练时间与训练数据量明显成线性关系
测试时间确实和理论一致，是Nlog(M)的时间复杂度。应该说这种时间复杂度的降低是我们使用KD树而不是原版的KNN最重要的地方。在原来的KNN算法下，假设训练集大小为M，测试集大小为N，则查询时间复杂度可以达到O(MN)，但是我们降低到O(Nlog(M))，还是挺合算的。
本次实验可以优化的地方很多，但是时间匆忙，没有做更深的扩展。欢迎大家提出更多建议。